Normal distribution: what is it, characteristics and examples in statistics?

The normal or Gaussian distribution is a concept widely used in statistics and psychometrics.

In statistics and probability, the normal distribution, also called the Gaussian distribution (after Carl F. Gauss), Gaussian distribution or Laplace-Gaussian distribution, reflects how data are distributed in a population.

It is the most common distribution in statistics, and is considered the most important because of the large number of real variables that take its form. Thus, many of the characteristics in the population are distributed according to a normal distribution: intelligence, anthropometric data in humans (e.g. height, stature...), etc.

Let's see in more detail what the normal distribution is, and several examples of it.

What is the normal distribution in statistics?

Normal distribution is a concept belonging to statistics. Statistics is the science that deals with the counting, sorting and classification of data obtained from observations, in order to make comparisons and draw conclusions.

A distribution describes how certain characteristics (or data) are distributed in a population.. The normal distribution is the most important continuous model in statistics, both because of its direct application (since many variables of general interest can be described by this model) and because of its properties, which have allowed the development of numerous statistical inference techniques.

The normal distribution is therefore a probability distribution of a continuous variable. Continuous variables are those that can take any value within an interval that is already predetermined. Between two of the values, there can always exist another intermediate value, susceptible to be taken as a value by the continuous variable. An example of a continuous variable is the weight.

Historically, the name "Normal" comes from the fact that for a time it was believed by physicians and biologists that all natural variables of interest followed this model.

Characteristics

Some of the most representative characteristics of the normal distribution are as follows:

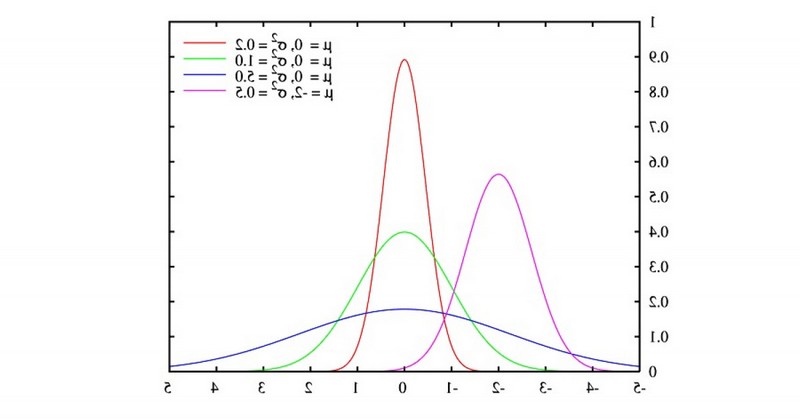
Mean and standard deviation 2.

To the normal distribution corresponds to a mean of zero and a standard deviation of 1.. The standard deviation indicates the separation that exists between any value of the sample and the mean.

2. Percentages

In a normal distribution, it can be determined exactly what percentage of the values will fall within any specific range. specific range. For example:

About 95% of the observations are within 2 standard deviations of the mean. 95% of the values will fall within 1.96 standard deviations from the mean (between -1.96 and +1.96).

Approximately 68% of the observations are within 1 standard deviation of the mean (-1 to +1), and about 99.7% of the observations would be within 3 standard deviations of the mean (-3 to +3).

Examples of Gaussian distribution

Let us give three examples to illustrate, for practical purposes, what the normal distribution is.

1. Height

Consider the height of all Spanish women; this height follows a normal distribution. That is, the height of most women will be close to the average height. In this case, the average Spanish height is 163 centimeters for women.

On the other hand, a similar number of women will be a little taller and a little shorter than 163cm; only a few will be much taller or much shorter.only a few will be much taller or much shorter.

2. Intelligence

In the case of intelligence, the normal distribution holds true worldwide, for all societies and cultures. This implies that the majority of the population has average intelligenceThe extremes (below, people with intellectual disabilities, and above, the gifted) are smaller parts of the population (approximately the same % below as above).

3. Maxwell curve

Another example that illustrates the normal distribution is the Maxwell curve. The Maxwell curve, within the field of physics, indicates how many gas particles are moving at a given speed..

This curve rises smoothly from low velocities, peaks at the mean, and descends smoothly again towards high velocities. Thus, this distribution shows that most of the particles move at a velocity around the average, a characteristic of the normal distribution (concentrating most of the cases at the mean).

Bibliographical references:

• Quintela, A. (2005). Estadística Básica Edulcorada. Bookdown.
• Fontes de Gracia, S. García, C. Quintanilla, L. et al. (2010). Fundamentos de investigación en psicología. Madrid: UNED. ISBN: 978843626260557.
• Botella, J. Sueró, M. Ximénez, C. (2012). Análisis de datos en psicología I. Madrid: Pirámide. ISBN: 9788436815382.